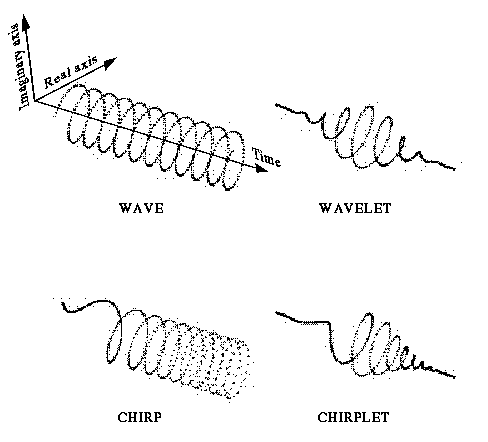
The chirplet is a windowed portion of a chirp. Four examples of chirplets (note for example, that a wave is a special case of a chirplet where the "chirprate" is zero and the window size is infinity).
In traditional signal processing, we use waves or wavelets. Waves are harmonic oscillations, such as sin(wt), where w is the frequency of the wave. ``Wavelets'' in the broadest sense are ``pieces of waves'', namely windowed waves. In a more strict use of the term, there are other mathematical restrictions such as the absence of a DC component.
The Chirplet Transform was invented in Canada in the 1980s and this work was
pubished in 1991 as
a recently-proposed alternative to waves and wavelets.
The chirplet is to a wavelet as the chirp is to a wave,
as shown in the figure below:

The chirplet is a windowed portion of a chirp.
Four examples of chirplets (note for example, that a wave is a special
case of a chirplet where the "chirprate" is zero and the window size
is infinity).
A chirp is a would-be harmonic function but instead of having a fixed period (or frequency=1/period) the period changes with position (or time, or the like) along the function.
The most notable examples of chirps are the sounds made by birds where the resonant cavity changes size while oscillating. A slide-whistle can also make a chirping sound, by virtue of a cotton ball on a piece of wire that allows the user to change the length of the active portion of the wistle while blowing on it.
@ARTICLE{mannVI91,
author = "Mann, Steve and Haykin, Simon",
title = "The Chirplet Transform: A Generalization of
{G}abor's Logon Transform",
journal = "Vision Interface '91",
publisher = "",
organization = "Canadian Image Processing and Patern Recognition Society",
address = "Calgary, Alberta",
month = "June 3-7",
pages = "205--212",
note = "ISSN 0843-803X",
year = "1991"
}
A scan of the 8 page article is here
and you can also
download a gzipped tarfile in html with
jpeg files if you'd like to mirror this portion of the site.
Copies of the full conference proceedings are obtainable from:
Canadian Information Processing Society 430 King St. West, Suite 205 Toronto, Ont. Canada M5V 1L5 Tel: (416) 593-4040The Gaussian chirplet transform in the above paper was inspired by Gabor's 1946 paper on communication.
This work was also published in 1991:
@ARTICLE{mannspieconference,
author = {Mann, Steve and Haykin, Simon},
title = "{The Adaptive Chirplet: An Adaptive Wavelet Like Transform}",
journal = "SPIE, 36th Annual International Symposium on Optical and
Optoelectronic Applied Science and Engineering",
organization = "The International Society for Optical Engineering",
address = "San Diego, California",
month = "21-26 July",
year = "1991"
}
The above paper describes Logon Expectation
Maximization (LEM) which is a form of EM
in the Time Frequency plane to form an
optimal set of chirplet functions for the
analysis of particular classes of signals.
There was also a 1992 paper on the Adaptive Chirplet Transform.
@ARTICLE{mannsp,
author = "Steve Mann and Simon Haykin",
title = "The Chirplet Transform: Physical Considerations",
journal = "{IEEE} Trans. Signal Processing",
year = "1995",
volume = 43,
number = 11,
pages = 2745--2761",
month = "November",
organization = "The Institute for Electrical and Electronics Engineers"}
# publisher = "{IEEE}",
# in above line, IEEE doesn't get included so i put it as part of the journal
Download:
HTML preprint version