- ...
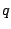 1
1
- Except in rare instances where the illumination
is so intense as to damage the imaging apparatus, as, for
example, when the sun burns through photographic negative film and
appears black in the final print or scan.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sense2
- In a typical imaging situation with 480 by 640
images and 256
grey values, this amounts to solving 307200 equations in
257 unknowns: 256 for F and one for K.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zero3
- This choice is arbitrary, as
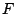 could have been
fixed at any point. However, it is common practice, when working
with logarithmic units, to define the maximum quantity as zero
(e.g. audio and video recorders typically have signal measurement
meters calibrated so maximum signal input corresponds to 0dB),
and since
could have been
fixed at any point. However, it is common practice, when working
with logarithmic units, to define the maximum quantity as zero
(e.g. audio and video recorders typically have signal measurement
meters calibrated so maximum signal input corresponds to 0dB),
and since 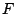 is assumed to be monotonic, the constraint
makes
is assumed to be monotonic, the constraint
makes 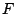 entirely negative when images are of increasing
exposure (
entirely negative when images are of increasing
exposure (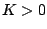 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
images4
- This summation over level sets is reminiscent of Lebesgue
integration (e.g. the form of summation
in (15) is to the earlier form of
the summation given in (9) as
Lebesgue integration is to Riemann integration, so we
will call it ``Lebesgue summation''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
multiplication5
- Also known as element-by-element multiplication
and denoted by ``.*'' in Octave, or nonstandard
proprietary work-alikes such as Matlab.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.