


Next: Robust statistics and yet
Up: Estimating camera response function
Previous: Smoothness and monotonicity constraints
The least squares formulation of (13)
can be solved using the standard approach for the normal equations.
Debevecdebevec presented a similar least squares
formuation, but his was much more computationally intensive because he
introduced extra unnecessary variables corresponding to our 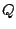 for
each exposure. Due to his large number of unnecessary variables he was
forced to use a small number of hand-selected points to calculate
a computationally tractable solution.
for
each exposure. Due to his large number of unnecessary variables he was
forced to use a small number of hand-selected points to calculate
a computationally tractable solution.
In contrast, our method (and earlier methods such as that of [2])
is computationally tractable, such that it uses the information at all the
pixels and hence could be expected to be much more immune to noise.
Our method
is also fully automatic and does not require any hand selection of image
portions in order to make it computationally tractable.
The method presented in this paper can be be made more efficient
(typically hundreds of times more efficient than it already is)
by the following:
- Recognizing that many rows of
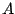 are repeated, these
rows can be grouped together into a single row
and weighted by the square
root of the number of repetitions. By weighting
are repeated, these
rows can be grouped together into a single row
and weighted by the square
root of the number of repetitions. By weighting 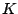 also by the same factor, the same numerical solution results.
also by the same factor, the same numerical solution results.
- Rows that are zero, which happen when the corresponding pixel
location in both images has the same value, may be eliminated,
further reducing the size of the matrix
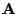 .
.



Next: Robust statistics and yet
Up: Estimating camera response function
Previous: Smoothness and monotonicity constraints
Steve Mann
2002-05-25